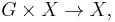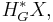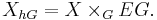Equivariant cohomology
In mathematics, equivariant cohomology is a theory from algebraic topology which applies to spaces with a group action. It can be viewed as a common generalization of group cohomology and an ordinary cohomology theory.
Specifically, given a group  (discrete or not), a topological space
(discrete or not), a topological space  and an action
and an action
equivariant cohomology determines a graded ring
the equivariant cohomology ring. If  is the trivial group, this is just the ordinary cohomology ring of
is the trivial group, this is just the ordinary cohomology ring of  , whereas if
, whereas if  is contractible, it reduces to the group cohomology of
is contractible, it reduces to the group cohomology of  .
.
Contents |
Outline construction
Equivariant cohomology can be constructed as the ordinary cohomology of a suitable space determined by  and
and  , called the homotopy orbit space
, called the homotopy orbit space
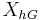 of
of 
on  . (The 'h' distinguishes it from the ordinary orbit space
. (The 'h' distinguishes it from the ordinary orbit space  .)
.)
If  is the trivial group this space
is the trivial group this space 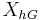 will turn out to be just
will turn out to be just  itself, whereas if
itself, whereas if  is contractible the space will be a classifying space for
is contractible the space will be a classifying space for  .
.
Properties of the homotopy orbit space
- If
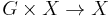 is a free action then
is a free action then 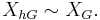
- If
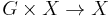 is a trivial action then
is a trivial action then 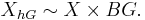
- In particular (as a special case of either of the above) if
 is trivial then
is trivial then 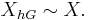
Construction of the homotopy orbit space
The homotopy orbit space is a “homotopically correct” version of the orbit space (the quotient of  by its
by its  -action) in which
-action) in which  is first replaced by a larger but homotopy equivalent space so that the action is guaranteed to be free.
is first replaced by a larger but homotopy equivalent space so that the action is guaranteed to be free.
To this end, construct the universal bundle 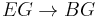 for
for  and recall that
and recall that 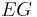 has a free
has a free  -action. Then the product
-action. Then the product 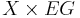 —which is homotopy equivalent to
—which is homotopy equivalent to  since
since 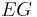 is contractible—has a “diagonal”
is contractible—has a “diagonal”  -action defined by taking the
-action defined by taking the  -action on each factor: moreover, this action is free since it is free on
-action on each factor: moreover, this action is free since it is free on 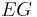 . So we define the homotopy orbit space to be the orbit space of this
. So we define the homotopy orbit space to be the orbit space of this  -action.
-action.
This construction is denoted by
References
- Hazewinkel, Michiel, ed. (2001), "Equivariant cohomology", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=e/e036090
- Tu, Loring W. (March 2011). "What Is . . . Equivariant Cohomology?". AMS Notices 58 (03): 423–426. http://www.ams.org/notices/201103/rtx110300423p.pdf.
Further reading
- Equivariant cohomology and equivariant intersection theory [1], Michel Brion